研究了包含卡普托导数的分数阶次扩散方程的区域梯度可观测性。该问题包括描述一种在空间域中包含的期望区域中查找和恢复初始梯度向量的方法。在给出必要的概念和定义后，我们证明了精确和近似区域梯度可观测性的一些有用的表征。给出了一个分数系统的非(全局)梯度可观测但区域梯度可观测的例子，说明了区域分析的重要性。对于两种类型的战略传感器，我们给出了区域梯度可观测性概念的表征。初始梯度的恢复采用Hilbert唯一性方法的展开进行。给出了两个示例来说明所开发方法的应用。数值模拟结果表明，该算法在重构误差方面是有效的。
分布式参数系统(DPS)的研究在科学和工程中催生了许多有用的概念，包括众所周知的稳定性、可控性和可观察性[1,2,3,4,5,6]。这些概念使人们能够更好地理解所研究的系统，增强控制系统的能力。所有这些概念都很重要，也有其特殊性，但在这里我们只关注可观测性的概念，该概念是卡尔曼于1960年首次引入的有限维系统[7]。目标是使用所考虑的系统的输出参数或测量值来恢复初始未知状态。在卡尔曼的开创性工作之后，可观测性的概念也被发展到涵盖无限维系统[8,9]。
在20世纪90年代，El Jai等人引入了一个更一般的概念，称为区域可观测性[10,11,12]。其主要目标是寻找和恢复所研究的分布参数系统的未知初始向量，但仅在空间域的部分区域内。当所考虑的系统在整个空间域无法(全局)观测时，区域可观测性的关键优势就变得清晰起来。在这种情况下，所研究的系统可以在一些精心选择的子区域进行区域观察。因此，我们至少可以部分地恢复初始状态，这在许多科学领域可能是有用的[13]。
图1
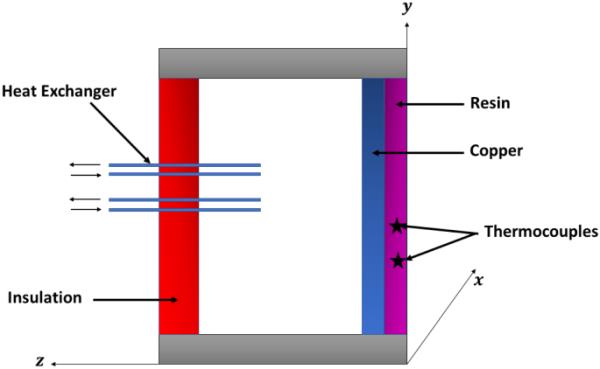
活动板块的轮廓
在引入区域可观测性概念后，Zerrik, Badraoui和El Jai提出了区域边界可观测性的概念，其目标与区域可观测性相同，但期望的子区域是边界的一部分[14,15]。虽然很重要，但所有这些概念和结果都不足以得到DPS的所有可能特征。因此，在21世纪，人们引入并研究了区域梯度可观测性的概念，目的是寻找并恢复合适区域的初始梯度向量[16,17]。我们在这里采用了梯度可观测性的概念，这一概念最近引起了人们的兴趣[18,19,20]。这是因为梯度可观察性的概念在现实生活中得到了应用。例如，考虑在稳定状态下发展的加热垂直板的边界上确定层流通量的问题:如图1所示为活动板的剖面。在这种情况下，梯度可观测性的概念与确定由加热板产生的热传递的问题有关。关于这一主题的更多信息，以及不同可观测性概念在各种系统中的应用，我们请读者参考[21,22,23,24]。
分数阶微积分是当今数学中发展最为迅速的领域之一，特别是使用分数阶系统来模拟现实世界的现象[25,26,27,28,29,30]。众所周知，分数阶算子、非整数阶微分算子和非整数阶积分算子具有许多突出的性质，使它们具有丰富的成果，适合描述和研究现实世界某些问题的特征。非局部分数算子不仅考虑局部点来计算某些函数的(分数)导数，而且还考虑过去的状态，如左侧分数算子的情况，或未来的状态，如右侧算子的情况。我们还提到分数算子具有遗传性质[31,32]。此外，分数算子的多样性也可以被视为分数微积分的一个优势，因为有许多不同类型的分数积分和导数导致在现实世界现象的建模中有更多的选择。这就解释了为什么分数阶微积分已经成功地应用于不同的领域。欲了解更多细节，我们建议感兴趣的读者参阅相关书籍[33,34]。
在区域可观测性的主题中，我们已经可以找到一些处理分数系统的作品[35,36,37,38,39,40,41]。然而，对时间分数扩散过程的区域梯度可观测性的研究很少。我们只知道[18]，Ge, Chen和Kou提出了Riemann-Liouville分数时间扩散过程的重构程序。本文的主要目的是研究由Caputo导数描述的时间分数扩散系统的区域梯度可观测性，其目的是在进化域的期望子区域中找到和重建被考虑系统的初始状态的梯度。这与[18]相反，在[18]中，非整数阶系统是用黎曼-刘维尔导数来写的，并且提到他们的方法无法涵盖卡普托导数所描述的系统(参见[18]的引理7)。在这里，我们证明了一个替代引理，它修复了[18]中提到的缺陷。我们的贡献包括给出考虑的线性系统的区域精确和近似梯度可观测性的几个特征。我们提出了一种方法，允许在期望的子区域的初始梯度向量的区域重建。此外，我们提供了一些简单的数值模拟来支持我们的理论结果。
本文的组织方式如下。在第2节中，给出了关于区域梯度可观测性的必要背景信息，以及它的一些有用的性质和特征。第3节将通过一个反例来说明，我们可以有一个系统，它不是梯度可观测的，但它在演化空间中某些合适的区域是区域梯度可观测的。然后，在第4节中给出了通过梯度策略传感器对手头概念的完整表征，而在第5节中，我们制定了为实现区域通量重建而应遵循的步骤。在第6节和第7节中，我们分别给出了所得结果的两个应用和两个成功的数值模拟。最后，我们以第八节的结论和未来的研究方向作为结束语。
我们现在提出了所考虑的初始梯度重建问题的一般公式。我们还布置了所有需要的初步结果和成分，以便读者能够顺利地跟随稿件。
设中有连通、开放和有界的集合，具有一个lipschitz -连续边界。最后一次，我们指定和。让我们将所考虑的系统的动态看作在状态空间中定义为的以下算子
（1）
式中为，各系数满足以下假设:
：
；
：
这样:
For和where。
假设和均值分别是，A是对称的和一致椭圆的。在这种情况下，已知有一组特征值，使得(见[42]):
每个特征值对应于特征函数，其中是，的多重性，使得和，和。进一步，该集合构成E的一组标准正交基。
算子A是E上的-半群的无穷小发生器，表示为:
（2）
在这里，我们研究具有以下形式的分数系统:
（3）
这里是u的分数阶导数，在卡普托的意义上，是欧拉函数。因为它的值和梯度都是未知的。系统(3)有且只有一种温和解，其形式如下:
（4）
式中为单参数Mittag-Leffler函数[43]。
不失一般性，我们取。输出函数提供了考虑系统的测量和信息，为:
（5）
对于[44]，算子满足以下允许条件:
（6）
希尔伯特空间被称为观察空间。
(4)中定义的算子是一个线性有界算子，参见[44]，它描述了所考虑的时间分数系统以初始状态为函数的演化。并且，如果算子C是有界的，则可容许性条件(6)总是满足，这意味着任何有界的观测算子都是可容许的观测算子。
让我们成为理想的次区域。我们引入以下限制运算符:
它们的伴随函数，
将式(4)代入式(5)得:
其中为可观测算子，它对区域和区域梯度可观测性的定义和表征都有重要贡献。在[34]中，C的可容性假设使得as的伴随数可以表示为:
(7）
设为梯度算子，对于所有v in。如[45]所示，其伴随数为-散度，即，
初始状态可以分解为:
区域梯度可观测性的目的是重建梯度向量。
我们记得，系统(3)与(5)增广称为精确(分别，近似)可观察，当且仅当(分别，)。根据文献[16]的讨论，我们表示并阐明以下定义:
系统(3)经(5)增广后，在(G表示梯度)中正好是G可观测的，如果
（8）
系统(3)经(5)增广后，在其中近似为g可观测
(9)
在特殊情况下，分数系统的定义1和定义2与经典系统的标准概念一致[16]。
现在我们给出一些有用的结果和性质。我们的第一个结果给出了近似区域梯度可观测性的表征。
下面的断言是等价的:
1 -
系统(3)近似为g可观测。
２－
=。
3 -
是肯定的。
4 -
.
结果证明，，和。
：
这是事实的直接后果。
：
让我进去吧。然后,
而且，我们知道，
使用2)，我们有:
因此，是肯定的。
：
让我们这样考虑，对所有人来说。因此，通过选择，我们得到了这个
因此，3)意味着。
：
让。我们做到了，这意味着所有人。因此，对所有人来说。因此，4)意味着，我们得出结论。
证据是完整的。
在证明第二个结果之前，我们回顾一下下面的引理。
(见[1])设F、G、E为三个自反巴拿赫空间。让我们考虑和。下面的断言是等价的:
1.
；
2.
这样:
下一个命题描述了精确的区域梯度可观测性。
上述语句是等效的:
1 -
系统(3)正好是g可观测的;
２－
=and关闭;
3 -
存在满足的:
我们证明了，和。
：
由于系统(3)正好是G-observable in，它也近似于G-observable in。因此，和。因此，和是封闭的。
：
由等式可知(3)近似于g可观察到。这一点，加上它是封闭的这一事实，意味着。因此，系统(3)正好是g可观测的。
：
系统(3)正好是g可观测的。我们已经知道这一点，因此剩下的就是证明这一点。最后一个包含是引理5的直接应用，有，，和
证据是完整的。
我们的命题4和6推广了[16]的主要结果，这些结果只对经典的整阶情况有效。
为了说明区域梯度可观测性的重要性，我们现在给出一个系统的例子，它不是近似梯度可观测的，但它是近似g可观测的。
让我们用时间分数系统来计算
（10）
连同输出
(11)
在哪里和。
的特征值和特征函数表示为:
和
此外，由(4)和(11)可知:
（12）
让我们成为…的一个元素。
梯度h不近似于g可观测值in，但近似于g可观测值in。
首先，让我们证明h不是g的近似可观测值，即对于所有。我们有:
因此,。
我们现在证明h近似于g，即，对于所有。我们有:
我们得出h近似于g在。
在本节中，我们给出了当所考虑的系统在期望的子区域近似为g可观察时，策略梯度传感器的特征。
我们称传感器为任何元件(D, f)，其中D是传感器的几何位置，它包含在，是它的分布。
这里我们介绍两种类型的传感器:
区域传感器，当D为正勒贝格测度时，空间为，测度为;
点向传感器，当，狄拉克质量以b为中心，空间为，输出方程为。
当我们考虑区域传感器时，观测算子是有界的;如果取点向传感器，则观测算子是无界的，但它是允许观测算子。
有关传感器及其特性的更多信息，请参见[34,46,47]。
让我们重新考虑系统(3)。我们采用由p个传感器给出的测量。观测空间为，输出方程为:
（13）
在哪里。观测算子C的伴随数表示为:
（14）
对于区域传感器的情况，由
（15）
对于点传感器来说。
如果(3)与(13)增广后近似于G-observable in，则传感器序列(或传感器)被称为梯度策略。
在[18]中，给出了一个引理([18]的引理7)，当所考虑的系统以Caputo导数的形式写成时，它就失效了，就像我们在这里做的那样。现在，我们提出另一种新的引理来处理这个问题。
本文的问题只用卡普托型分数阶导数来表述。然而，Riemann-Liouville分数阶导数由于分数分部积分和Green公式(参见引理14和15)而自然出现。
设r是一个满足
（16）
地点:
是Riemann-Liouville意义上的右侧分数阶导数，
是右边的Riemann-Liouville分数积分。那么下面的等式成立:
式(16)的解为:
式中是用概率密度函数定义的线性有界算子[44]。由[44]的命题3.3可知:
因此，由(7)，我们得到:
并对结果进行了验证。
下面的分数阶分部积分公式在后面的部分会很有用。
[见[48]]设v为in的函数，设u为AC(0, T;E)和[0,1]。这个公式
(17)
分部积分法成立。
我们的下一个结果(定理16)提供了梯度策略传感器的有用特征。为了证明它，我们利用式(17)和下面的分数格林公式。
[分数格林公式[44]]对于任何一个
（18）
序列是梯度策略的，当且仅当，
在哪里
和
从命题4中，我们得到梯度策略当且仅当，
这意味着，通过引理13，
（19）
其中r是(16)的解。现在让我们找出的确切表达式。让我们成为一个元素。我们介绍该系统:
（20）
其独特的温和解决方案被写成:
(16)两边同时乘以积分，得到
(21)
另一方面，式(17)给出:
(22)
由式(18)、式(21)、式(22)，利用边界条件，可得:
(23)
在不失去一般性的情况下，我们继续对区域传感器的情况进行证明(对于点传感器也可以很容易地做到这一点)。我们有:
(24)
利用式(19)、式(23)和式(24)，我们推导出梯度策略当且仅当，
从[18]中的引理5，我们得到最后一个表达式等价于，
这也等价于，
因为为了所有人，为了所有人，我们有:
并对结果进行了验证。
下面的推论是定理16在一维情况下的直接推论，即当。
如果，则是梯度策略，当且仅当，
；
对所有人来说。
摘要
1 介绍
2 问题陈述和区域
Nal梯度可观测性
3.一个反例
4 梯度策略传感器
5 的部位
信号梯度探测
nstruction方法
6 应用程序
7 数值模拟
8 结论
数据和材料的可用性
代码的可用性
参考文献
致谢
作者信息
道德声明
搜索
导航
＃＃＃＃＃
现在我们给出了一种方法的步骤，该方法允许恢复(3)的初始梯度。我们的方法是分数系统的Hilbert唯一性方法(HUM)的扩展。
让
注意这一点。
对于K中的每一个，我们引入这个系统:
(25)
它有且只有一个温和的解，写成如下:
（26）
我们联想到的形式:
(27)
其中的标量积是。
双线性形式满足共轭对称和正性质，即，和。
如果系统(25)在中近似为g可观测，则双线性形式(27)成为K上的标量积。
通过注释19，我们只需要证明它是确定的，即。
设f是k的一个元素，
这意味着:
使用注释18，这意味着:
并且，由于(25)近似于g，我们有。我们得出结论。这是根据事实得出的结论。
是K上的范数，我们用K表示它的完备性是范数。空间K现在是一个希尔伯特空间。
我们介绍以下辅助系统:
(28)
由(25)的溶液控制。
这个条件意味着系统(28)是系统(25)的伴随系统。
我们现在定义一个算子它关联到每一个可能的候选初始梯度，在K上的投影，
(29)
这样，区域梯度重建问题就简化为方程的可解性问题:
(30)
这引出了下一个结果。
如果系统(3)近似为g可观测值in，则式(30)有一个唯一解，对应于初始梯度in。
我们将证明它是强制的，也就是说，存在对所有的验证。在K中，
从[44]中的命题3.3中，我们得到了这个
因此,
(31)
式(30)只有一个解。
在本节中，我们采用。让我们成为理想的次区域。我们考虑以下时间分数系统:
（32）
我们的目标是说明在子区域中恢复初始梯度向量的步骤。我们介绍了第4节中介绍的两种类型传感器的方法。的特征值和特征函数为:
而且,
取一个带和的区域传感器(D, f)，
该传感器(D, f)是梯度策略，当且仅当，
在那里,
而且,
在本例中，，和。因此,
我们可以看到:
而且,
因此，利用定理16，(D, f)是梯度策略，当且仅当，
也就是说，当且仅当，
证据是完整的。
现在让我们来介绍一下:
使用引理20，对于any和in，表达式:
定义一个标量积，当系统(32)近似为g时，
是相关的范数。根据式(14)，我们可以将伴随系统写成:
由定理22可知，方程有且只有一个解。
现在我们重新考虑系统(32)，但增加了输出:
(33)
其中为传感器位置。因此，由式(4)和式(33)，我们有:
注意，点向传感器有一个无界观测算子。因为对所有人来说，是连续的，并且这样(见[34])。因此，点向传感器满足容许条件(6)。
点向传感器是梯度策略，当且仅当，
类似于23号提案的证明。
对于任意in，若系统(32)近似为G-observable in，则:
中定义规范。我们来写下伴随系统:
根据定理22，方程有且只有一个解。
在本节中，我们通过两个例子来说明解决梯度重建问题所采用的方法的有效性。为了求解式(30)，我们计算某个标准正交基的算子分量，表示为:
我们知道这是e的一组标准正交基，然后，通过设，在第k位，我们得到这是一组标准正交基。从现在开始，通过重新排列这些项，我们用。这是可能的，因为映射:
是1比1。式(30)现在可以近似为
(34)
With, and。我们知道:
(35)
由式(31)和式(35)可得:
综上所述，重构方法由算法1给出。
在第一个例子中，我们采用并考虑以下时间分数系统:
(36)
其中，输出函数与传感器对应。我们设为期望的子区域和将在其中重构的初始梯度向量，而假设未知的初始状态为。在实现本文提出的算法(算法1)后，得到重构的初始梯度。从图2中可以看出，初始梯度矢量与恢复梯度矢量的两幅图在期望区域内相邻，重构误差为:
图2
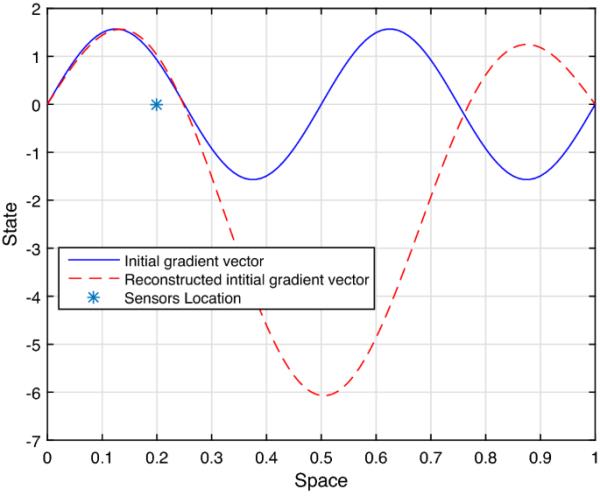
在7.1节的例子中，初始梯度向量和重构后的梯度向量
这表明数值方法是成功的。我们注意到所提出的算法没有考虑外的初始梯度值。
图3描述了根据传感器的位置误差演变的方式。如图所示，在许多位置误差很大，甚至达到无穷大。在这种情况下，我们说传感器是非战略性的。此外，很明显，传感器的最佳位置，在它给出最小重建误差的意义上，是。
图3
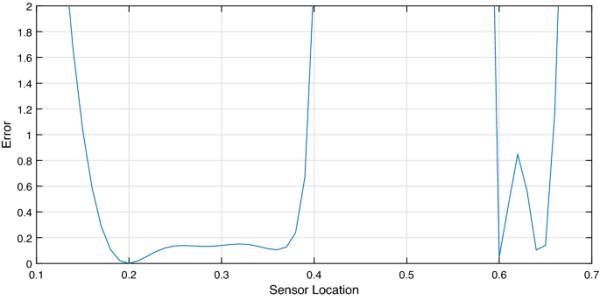
对于7.1节的例子，重构误差与传感器位置的关系
现在让我们考虑下面的分数制:
（37)
用区域传感器(D, f)与、、和子区域进行测量。我们选择初始状态为，待恢复的梯度为，这两个都是未知的。我们在图4中看到，初始梯度矢量的图与重建的初始梯度图几乎相同。实际上，重构误差的值为:
图4
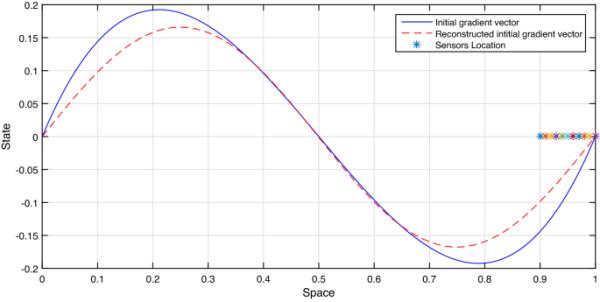
在7.2节的例子中，初始梯度向量和重构后的梯度向量
从这两个例子中可以看出，与考虑点向传感器的情况相比，区域传感器的情况给出的数值结果具有更好和更小的重建误差。这可能是由于这样一个事实，在这种情况下，传感器具有有界观测算子和具有非消失勒贝格测量的几何支持，这意味着与点向传感器的情况相比，测量值在更大的集合中给出，点向传感器的测量值在单个点b中提供，这意味着在这种情况下获得的测量量要少得多。因此，在有界观测算子的情况下，人们比无界观测算子拥有更多关于系统的信息。这些评论是基于所提出的算法实施过程中的观察结果，但需要更多的理论研究，关于战略传感器的理论，从理论上证实和验证我们的数值模拟的观察结果。
研究了用卡普托导数给出的线性时间分数系统的区域梯度可观测性问题。我们开发了一种方法，使我们能够获得所需区域的初始梯度向量。我们还利用梯度策略传感器给出了区域梯度可观测性的完整表征。尽管我们研究了传感器的两种特殊情况，即点向和区向，但对于其他类型的传感器，例如灯丝传感器，也可以得到类似的结果。本文给出的数值模拟结果在错误率和计算时间方面都令人满意。我们使用Matlab R2014b软件在具有8 GB RAM的2.5GHz酷睿i5计算机上实现了所考虑的示例。
HUM方法的优点在于它可以在数值上进行模拟，提供了对误差控制满意的区域初始梯度。此外，它可以适应现实世界的应用程序。在将这种方法应用于示例时，可能面临的一个缺点是，当考虑具有无限多重特征值的动态a时。在这种情况下，人们需要无限数量的传感器来观察系统，这在现实中是永远无法实现的。对于未来的工作，我们计划将本文的结果扩展到半线性分数系统的情况。在数值模拟方面，我们考虑了一些学术实例，以说明所获得的理论结果。我们声称我们的结果可以应用于现实世界的情况，这个问题将在其他地方讨论。
下载原文档：https://link.springer.com/content/pdf/10.1007/s40435-022-01106-0.pdf