工程、生物技术、能源等应用产生的数据的快速增长已经成为高维数据挖掘的一个关键挑战。大量的数据,特别是高维数据,可能包含许多不相关的、冗余的或有噪声的特征,这可能会影响工业数据挖掘过程的准确性和效率。近年来,一些元启发式优化算法被用来发展特征选择技术来处理大维问题。尽管优化算法能够在搜索空间中找到接近最优的特征子集,但它们仍然面临一些全局优化的挑战。为了提高高维工业优化问题的搜索性能,本文提出了一种改进版的灰项优化算法,即ST- al方法。ST-AL方法通过采用四种策略来提高STOA的性能。第一种策略是使用控制随机化参数,以确保在搜索过程中探索-开发阶段之间的平衡;此外,它避免了陷入局部最优。第二种策略需要基于蚂蚁狮子(AL)算法创建一个新的探索阶段。第三种策略是通过修改位置更新主方程来改进STOA开发阶段。最后,利用贪心选择法忽略产生的贫困人口,使其不偏离已有的有发展潜力的地区。为了评估所提出的ST-AL算法的性能,我们采用ST-AL算法作为全局优化方法来发现十个CEC2020基准函数的最优值。将其作为一种特征选择方法应用于UCI知识库中的16个基准数据集,并与7种知名的优化特征选择方法进行了比较。实验结果表明,该算法在避免局部极小值和提高收敛速度方面具有优势。将实验结果与ALO、STOA、PSO、GWO、HHO、MFO、MPA等算法进行了比较,得到的平均精度在0.94 ~ 1.00之间。
在过去的几十年里,优化问题在几个领域引起了广泛的关注,仅举几例:计算机科学、工程、运筹学、能源和商业(Oliva和Elaziz 2020)。通常,优化技术旨在从问题搜索空间中的一组可用替代方案中确定最佳解决方案。优化问题可以分为二元或连续,静态或动态,单目标或多目标,约束或无约束(Hussien和Amin 2021)。在复杂的优化问题中,必须根据问题类型对搜索空间进行充分的研究(Anand and Arora 2020)。因此,由于优化问题的复杂性和类型的多样性,传统的数学技术(例如牛顿和梯度下降)由于其大量的时间和落入局部最优问题的概率而变得毫无价值(Hussien和Amin 2021)。
元启发式技术已经成功地发展起来,可以有效地处理许多棘手的优化问题。他们有能力从搜索空间中挖掘重要信息,并快速有效地确定最佳解决方案(Anand and Arora 2020)。几乎所有的元启发式算法都受到自然的启发,比如动物、鸟类、昆虫甚至人类的行为(Hussien and Amin 2021)。遗传算法(GA) (Goldberg and Holland 1988)、粒子群优化(PSO) (Eberhart and Kennedy 1995)、差分进化(DE) (Storn and Price 1997)、萤火虫算法(Yang 2010)、传粉算法(FPA) (Yang 2012)、人工蜂群(ABC) (Karaboga and Basturk 2007)和灰狼优化算法(GWO) (Mirjalili et al. 2014)是原始和突出的元启发式算法的例子。最近,有几个自然启发的元启发式技术已经被创新,仅举几例,蚱蜢优化算法(GOA) (Mirjalili等人,2018),自私群体优化器(SHO) (Fausto等人,2017),蜜獾算法(HBA) (Hashim等人,2022),蝴蝶优化算法(BOA) (Arora和Singh 2019),正弦余弦算法(SCA) (Mirjalili 2016), Salp群算法(SSA) (Mirjalili等人,2017)和蛇优化器(SO) (Hashim和Hussien 2022)。
首先,元启发式算法包含两个基本阶段:探索和利用。探索阶段通常基于用于在搜索空间中有效搜索的随机化方法。同时,开发阶段关注的是寻找搜索空间中最有希望的区域。另一方面,在高维数据集上进行知识发现是至关重要的。它需要通过预处理数据阶段来准备数据(Anand and Arora 2020)。这一预处理步骤主要用于通过忽略和剥离数据集中不相关、冗余、缺失和噪声特征来降低高维数据的维数(Sayed等人,2018)。通常,特征选择过程被认为是应对维数诅咒的重要数据预处理方法。特征选择策略旨在根据一组标准选择特征子集,同时保持原始特征的物理含义(Huang et al. 2020)。特征选择过程可以通过减小搜索空间大小来增强学习模型的理解和感知,从而提高学习效率(即减少训练时间和分类器复杂度,提高预测性能或分类精度)(Zhang et al. 2014)。
通常,基于用于评估特征子集的方法,特征选择方法分为三类:过滤器、包装器和嵌入方法(Neggaz et al. 2020)。数据的内在属性用于选择过滤方法的特征(Teng等人,2017)。过滤器方法被称为独立于分类器的方法,因为无论机器学习技术如何,它们都会评估用于分类的重要信息(Rani and Rajalaxmi 2015)。过滤方法很快,因为它们不使用学习算法来分析属性,但它们不能提供足够的信息来对样本进行分类。基于快速关联的过滤器(FCBF)和最小冗余最大相关性过滤器(mRMR)是两种过滤器类型。另一方面,包装器和嵌入式模型依赖于分类器。包装器模型使用机器学习技术研究潜在解决方案的空间(Emary et al. 2016)。为了评估选择的子集,使用某个分类器的验证精度。基于嵌入的方法在分类模型构建过程中发现哪些特征对分类模型的准确性影响最大。包装方法通常优于过滤器方法,因为所提出的特征子集是使用学习算法的反馈来评估准确性的。然而,在计算上,它们更昂贵,并且在性能方面,它们取决于应用的学习方法。
因此,特征选择算法的最关键方面是寻找最优或接近最优的特征子集,以提高分类器的准确性并降低计算复杂度。像广度搜索和深度搜索这样的穷举搜索方法被认为对于发现特征子集是不可行的,特别是在大量数据集中。一个包含M个特征的数据集需要产生2M个特征子集。需要评估这些特征子集的质量(Zhang et al. 2014),这是计算密集型的,特别是在基于包装的方法中,必须为每个子集实现学习算法。最好的方法是将特征选择视为NP-hard优化问题。目标函数最小化所选特征的数量,同时保持最高的分类精度。这意味着特征选择问题可以从元启发式中受益,元启发式在解决各种优化问题方面表现出非凡的性能(Motoda和Liu 2002)。元启发式算法具有动态搜索行为和全局搜索能力,能够解决复杂的优化问题。事实上,已经使用了几种元启发式算法来提高特征选择过程的性能,仅举几例,遗传算法(Oh等人2004),粒子群优化(Gu等人2018),蚁群优化(ACO)算法(Aghdam等人2009),人工蜂群(ABC)算法(Uzer等人2013),二元引力搜索算法(BGSA) (Papa等人2011),分散搜索算法(SSA) (Wang等人2012),阿基米德优化算法(AOA) (Desuky et al. 2021)、回溯搜索算法(BSA) (Ghanem and Layeb 2021)和蛾焰优化(MFO)算法(Soliman et al. 2018)。
大多数最初引入的优化技术通常都存在一些性能缺陷,特别是在大规模数据集中实现时。这些缺点是由于勘探和开采阶段不平衡,导致陷入局部最优或不能适当收敛。在这种情况下,最近的大多数特征选择文献都倾向于修改现有的元启发式算法以提高其性能,或者在不同的元启发式算法之间进行杂交,以利用一种技术来提高另一种技术的搜索效率。例如,哈里斯鹰优化(HHO)算法与模拟退火(SA)的杂交(Abdel-Basset et al. 2021),算法优化算法(AOA)与遗传算法(GA)的杂交(Ewees et al. 2021), salp群算法(SSA)与正余弦算法(SCA)的杂交(Neggaz et al. 2020),海鸥优化算法(SOA)与lsamvy飞行和变异算子的结合(Ewees et al. 2022)。
然而,这些方法有一些限制,会影响最终解决方案的质量。根据无免费午餐定理(No Free Lunch Theorem, NFL) (Wolpert and Macready 1997),得出在所有类别的特征选择问题上,没有一种算法优于其他算法的结论。因此,必须设计一种新的算法或现有算法的改进版本来更有效地处理特征选择挑战。这是我们提出一种新的特征选择方法的主要动机,该方法基于增强一种新的元启发式算法的性能,称为黑燕鸥优化算法(STOA) Dhiman和Kaur(2019)。这种改进是通过使用蚂蚁狮子优化(ALO) (Mirjalili 2015a)算法来增强对STOA的探索,因为ALO能够定位包含最优解的可行区域。
STOA算法是Dhiman和Kaur通过模拟自然界中海鸟黑燕鸥的迁徙和攻击行为,提出的一种新的基于种群的元启发式算法(Dhiman and Kaur 2019)。在过去的几十年里,它得到了很多关注,并被用于各种应用中(Ali et al. 2021;郑等,2021;Kader and Zamli 2022)。尽管有杰出的应用,STOA仍然需要更多的改进来克服其局限性。例如,STOA探索阶段仅基于最优解,这使得它无法正确地探索搜索空间,以找到包含最优解的突出区域。另一方面,ALO是Mirjalili (2015a)提出的流行的元启发式算法,其灵感来自蚁狮的狩猎机制。该算法具有勘探开发阶段好、避免陷入局部最优水平、最优解收敛速度快等特点。
在本研究中,提出了一种新的杂交技术,通过使用ALO算法提高STOA的性能。这种杂交称为ST-AL方法。通过两个实验对ST-AL方法的性能进行了评估;(1)解决全局优化问题;(2)解决特征选择挑战。本文的主要贡献可以概括为以下几点:
1.
提出了一种基于灰燕鸥优化算法(ST)和蚁狮优化算法(AL)的混合算法。该方法被称为ST-AL。
2.
在CEC 2020测试套件上测试ST-AL。
3.
采用ST-AL作为大型和小型基准数据集的包装特征选择算法
4.
将ST-AL算法与已有的群智能算法(如PSO、GWO、HHO、MFO、MPA以及传统的ST-AL算法)的性能进行比较
5.
验证了该方法在全局优化和特征选择问题上的有效性和优越性。
本文的其余部分组织如下:第2节对相关工作进行了详细概述。为了理解方法,关于算法的初步研究将在第3节中提出。第4节介绍了所提出方法的详细概述。本文算法的性能评估在第5节中给出。最后,在第6节中总结了工作的未来范围。
近年来,元启发式算法作为一种寻找最优解和改进特征选择过程的有效技术受到了人们的关注,特别是随着数据量和复杂性的大量增加。为了提高优化过程,一些研究开发了鲁棒的当前元启发式优化算法来克服样本解空间中的局部最优问题。例如,一些研究人员使用混沌搜索来增强搜索过程,解决局部最优问题和低收敛速度问题,如Arora等(2020)。本文提出了一种基于内部搜索算法与混沌理论相结合的混沌内部搜索算法(CISA),以解决局部最优和收敛速度慢的问题。为了评估所提出的算法,它已经在13个全局基准函数上进行了测试。Sayed等人也采用混沌理论提高Salp Swarm Algorithm (SSA)的性能,提出了混沌Salp Swarm Algorithm。本文采用了十种不同的混沌映射来提高收敛速度和结果精度(Sayed et al. 2018)。在Anand and Arora(2020)中,混沌搜索也促进了自私群体优化器(SHO)的搜索过程。Anand和Arora提出了一种混沌自利群体优化算法(CSHO),该算法使用各种混沌映射来替代每个搜索代理的生存参数值,从而有助于控制勘探和开发过程。同样,Oliva和Elaziz(2020)应用混沌映射和基于对立的学习(OBL)来增强头脑风暴优化算法(BSO)的性能。该算法被称为带干扰的对立混沌BSO (OCBSOD)。该算法的思想可以概括为以下几个步骤:首先,利用混沌映射计算初始解;然后,基于对立的学习在搜索空间中产生相反的位置,然后,识别最佳粒子并在迭代过程中应用。中断算子的作用是更新实例在种群中的位置。最后,应用OBL增强了搜索域的探索过程。
Harris hawks optimization (HHO)是受Harris的合作方式和追逐行为启发的另一种元启发式算法。通过将HHO与各种优化技术(如基于对立的学习、混沌局部搜索和Hussien和Amin(2021)的自适应技术)相结合,HHO的性能得到了提高。Wang等人(2021)也试图通过开发将HHO与Aquila Optimizer (AO)相结合的混合算法来提高HHO的全局优化搜索性能。
在同样的背景下,Long等人开发了Butterfly优化算法BOA的改进版本,采用自适应gbest引导搜索策略和基于针孔成像的学习,以克服在解决高维优化问题时可能出现的局部最优问题(Long et al. 2021)。在IEEE CEC2014的23个经典基准测试函数、30个复杂基准测试函数、CEC 2017的30个最新基准测试函数和21个特征选择问题上对该算法进行了研究。此外,EL-Hasnony等人(2021)通过将蝴蝶算法与粒子群算法相结合来改进蝴蝶算法,以提高其全局优化性能。在这项研究中,作者研究了该算法在COVID-19数据集上的性能。在Assiri(2021)中,混沌局部搜索和基于对立的算法也被集成到蝴蝶优化算法中,以获得最优或近最优结果。
Khaleel和Mitras(2020)也将基于模拟座头鲸觅食和迁徙行为的鲸鱼优化算法(Whale optimization algorithm, WOA)与改进的共轭梯度算法相结合。该混合算法基于推导一个新的共轭系数来提高全局优化问题的求解效率。在另一种情况下,由于其强大的全局搜索能力,WOA已被用于增强其他优化算法,如Che和He(2021)。本研究将WOA与Seagull优化算法(SOA)相结合,提出了SOA的改进版本,称为WSOA。热交换优化是另一种与SOA结合的优化算法,可以增强其开发能力,解决特征选择问题。其他一些类型的研究提出了各种优化技术之间的杂交,如Adamu等人(2021)的混沌乌鸦搜索和粒子群优化算法,Khamees和al -baset的正弦余弦算法和布谷鸟搜索(2020),萤火虫算法和差分进化(Zhang等人2016)。
从上述各项研究结果来看,优化算法的发展仍然值得进一步提高开发能力,解决全局优化问题,如收敛慢、计算精度低、陷入局部最优等问题。表1展示了最近应用杂交思想来增强元启发式优化算法和解决特征选择问题的研究。本文提出了一种新的方法,通过提高灰燕鸥优化算法(STOA)的性能,并将其与蚂蚁狮子算法(ALO)相结合,来挑选最具信息量的特征。
表1混合优化技术的最新方法
蚁狮优化器(ALO) (Mirjalili 2015a)是一个受生物学启发的优化器,它模拟了蚁狮在自然界中的行为。它们的狩猎行为非常独特和有趣。蚁狮建造了一个边缘锋利的锥形陷阱来诱捕蚂蚁。之后,他们躲起来,等待蚂蚁/昆虫被困住。锋利的边缘防止被困的昆虫逃脱,容易掉到陷阱的底部。最后,蚁狮吃掉昆虫,扔掉剩下的,为下一次捕猎准备陷阱。人们注意到,antlion的饥饿程度越高,它们挖的陷阱就越大。
蚁群算法试图解决蚂蚁寻找食物的随机行走、陷阱构建过程、蚂蚁的陷阱、捕获目标、陷阱重建等优化问题。这些在搜索空间上的随机移动使用累积和函数和通过不同迭代应用的随机函数来建模。这种随机行为迫使寻找全局最优解。在优化过程中采用目标函数来表示模型的目标,以有效地最大化资源的利用。ALO还假设蚁群隐藏在使用最小-最大算法限制的搜索空间中。ALO算法模拟了狩猎的主要五个步骤:(a)蚂蚁的随机行走,(b)陷阱的建立,(c)蚂蚁的陷阱,(d)滑动猎物到蚁狮,(e)抓取蚂蚁和陷阱的重建,如下所示:
1.
蚂蚁的随机行走。首先,初始化搜索景观中的蚂蚁种群,并将其位置存储在如下向量中:
(1)
其中是第i个蚂蚁,是第i个蚂蚁在DTH维中的位置。在优化的每一步中,每个蚂蚁在每个维度中的位置都使用随机游动来更新。
(2) (3)
其中cumsum为累积和,n为最大迭代次数,t为随机行走的步长/迭代,r(t)为随机函数,rand为均匀分布在[0,1]之间的随机数。利用最小-最大归一化将蚂蚁的随机行走限制在有限搜索空间的边界内,如下所示:
(4)
式中为变量i随机游走的最小值,为变量i随机游走的最大值,为变量i在迭代第t时的最小值,为变量i在迭代第t时的最大值。
2.
这个陷阱是用一个轮盘赌来选择蚂蚁,根据它们的健康状况。ALO假设蚂蚁只被困在一个选定的蚁笼中。蚁狮根据它们的适合度值建造更大的坑来捕捉昆虫/目标。蚁群对蚂蚁运动的影响建模如下:
(5) (6)
式中为迭代t时所有变量的最小值,为迭代t时所有变量的最大值的向量,为蚂蚁i时所有变量的最小值,决定了蚂蚁j在迭代t时的位置。
3.
建筑陷阱陷阱是用轮盘赌来选择狮子的健康状况。ALO假设蚂蚁只被困在一个特定的蚁笼中。蚁狮根据它们的适合度值建造更大的坑来捕捉昆虫/目标。
4.
当一只蚂蚁被困住时,蚁狮开始向坑的中心扔沙子,这样猎物就会滑进陷阱。在这一步中,使用方程自适应最小化随机游走的超球半径。(7)、(8)。
(7) (8)
其中I是一个比值,是迭代t时所有变量的最小值,是包含迭代t时所有变量的最大值的向量。
5.
捕捉猎物,重建洞穴。在这一步中,被捕获的蚂蚁被认为比相关的蚂蚁更健康。之后,蚁狮将自己的位置更新为被捕获猎物的最新位置,以增加捕获新猎物的机会。这一步用Eq.(9)进行数学建模。
(9)
其中t为当前迭代,Antlion为第t次迭代时蚂蚁j的位置,Ant为第t次迭代时蚂蚁i的位置。
6.
Elitism ALO在整个优化过程中保持最佳解决方案。在每次迭代中得到的最适合的蚁群被认为是精英。精英蚁群能够在迭代过程中影响所有蚂蚁的运动。因此,每只蚂蚁随机绕着轮盘赌和精英选择的蚁群行走,如下所示:
(10)
式中,为第t次迭代时轮盘赌围绕选定蚁群的随机游走,为第t次迭代时围绕精英蚁群的随机游走,为第I次迭代时蚁群的位置。
算法1给出了ALO算法的伪代码。

STOA算法的灵感来自于黑燕鸥的攻击/开发和迁徙/探索行为(Dhiman and Kaur 2019)。黑燕鸥以蚯蚓、昆虫、鱼、爬行动物等为食。它们群居生活,有着独特的迁徙和攻击行为。在迁徙(探索)过程中,黑燕鸥成群迁徙,寻找和定位最富有的。在攻击过程中,黑燕鸥会飞向目标。它们通常在两只鸟之间保持距离,以避免碰撞。在群体中,鸟类会朝着最适合生存的方向飞行,并相应地更新自己的位置。STOA对搜索空间中开发和探索的数学符号建模如下:
1.
迁移/探索行为试图找到满足三个条件的搜索代理之间的距离:
(a)
每个代理和它的邻居之间的碰撞避免
(11)
其中为保证不与邻居发生碰撞的agent的位置,为搜索agent (st)在迭代z中的位置,为搜索agent在搜索空间中的移动。
(12)
其中,Max_iterations是一个控制变量,用于适应从0线性减少的变量。初始化为2。
(b)
向最佳邻居方向收敛避免碰撞后,搜索代理向最适合邻居的方向移动。
(13)
其中为agent在最佳agent方向上的位置,负责更好探索的随机变量计算如下:
(14)
式中为[0,1]范围内的随机数。
(c)
更新与最适合的搜索代理相关的信息,最终搜索代理根据最佳代理更新自己的位置。
(15)
搜索代理和最适代理之间的差距在哪里?
2.
攻击/利用行为黑燕鸥在攻击时调整速度和角度。在攻击目标/猎物时,它们会扇动翅膀以增加飞行高度,方法如下:
(16) (17) (18) (19)
式中为螺旋每转一圈的半径,I为范围内的变量,u和v为标识螺旋形状的常数,e为自然对数底。最终,agent更新后的位置计算如下:
(20)
其中计算其他agent的更新位置并保存最优解。
算法2给出了STOA算法的伪代码。

摘要
1 介绍
2 相关的工作
3.初步研究a
布特算法
4 提出了混合ST-AL优化算法
5 性能e
拟议ST-AL的估值
6 有限公司
结论和未来的工作
数据可用性
参考文献
作者信息
道德声明
搜索
导航
#####
本节解释了所提出的ST-AL方法的结构,该方法结合了STOA和ALO算法。在本文提出的ST-AL方法中,采用以下四种策略来提高STOA算法的性能:
控制随机化参数
基于ALO算法的新探索阶段
增强STOA开发阶段
贪婪的选择。
随机化是元启发式算法的一个主要方面,对平衡勘探开发阶段起着至关重要的作用,因此随机化的控制参数必须更精确,才能得到有希望的结果。在混合ST-AL方法中,提出了两个参数集成在一起来完成该任务。第一个参数控制随机化的值,称为随机化值(rv),由:
(21)
在控制随机化中提出的第二个参数称为随机化方向(rd)。rd参数的值为或,这使得有机会在给定的搜索空间中改变搜索代理的方向,从而对感兴趣的区域进行良好的扫描。(rv)和(rd)的结合可以很好地扫描给定的搜索空间,降低陷入局部最优和过早收敛的概率。
策略2:基于ALO算法的新探索阶段探索阶段的特点是运动步长较大,使算法能够覆盖给定的搜索空间。STOA的探索阶段不满足这一方面,因为智能体更新位置的过程仅基于群体中最佳智能体的位置和智能体的当前位置。因此,在给定的搜索空间中,它无法在不同的区域进行大的移动。在ST-AL方法中,勘探阶段基于ALO算法。
ALO算法具有良好的探索策略,该策略基于蚁群(排序代理)的随机选择和蚁群(代理)周围的随机行走。每只蚂蚁同时随机绕过由轮盘和精英(最适合的蚂蚁)选择的蚁群,如下所示:
(22)
式中为迭代t中搜索代理的位置,为围绕轮盘赌选择的代理的随机游走,为围绕最佳代理的随机游走。
因此,所提出的ST-AL方法的探索阶段遵循相同的策略,获取和,然后更新agent的位置如下:
(23)
在更新方程中加入,用于引导具有当前位置且不变化于错误位置的agent。控制随机化参数,是一个用于平衡勘探与开采的绝对值,其值随时间逐渐变化。
在本文提出的混合ST-AL方法中,利用阶段与原始STOA算法中的利用阶段策略相似,只是对位置更新方程进行了一些设置,以提高其效率。ST-AL的开发阶段可以概括如下:
1.
避碰。这里不发生碰撞的代理定义为:
(24)
其中为不与其他搜索代理发生冲突的搜索代理的位置。表示搜索代理在给定搜索空间内为避免其相邻搜索代理之间的避碰而进行的移动,计算公式为:
(25)
式中为[0,2]之间的控制变量(在本研究中),T为总迭代时间,T为当前迭代。
2.
向最佳邻居的方向收敛。避碰后,agent收敛到最佳agent,其数学定义为:
(26)
式中为搜索代理的不同位置,为由式给出的随机数:
(27)
其中为随机数[0,1]
3.
更新相应的最佳搜索代理。为当前代理商与最佳代理商之间的差距,给出如下:
(28)
4.
在空气中的螺旋行为。迁移后,各agent的螺旋运动如下:
(30) (31) (32)
式中,表示空气中的螺旋行为,为螺旋每转一圈的半径,I为变量,u和v为螺旋运动形状的常数。
5.
更新搜索代理位置。最后,代理更新自己的位置如下:
(33)
哪里是群中最好的agent。取绝对值是为了消除无效的随机化,避免偏离全局最优。rv和rd是由式(21)给出的控制随机化参数。
策略4:贪心选择在生成的种群和当前种群之间进行贪心选择,拒绝生成的较差的种群,避免算法偏离已有的有希望的区域。所提出的ST-AL方法流程图如图1所示,伪代码在算法3中给出。

图1
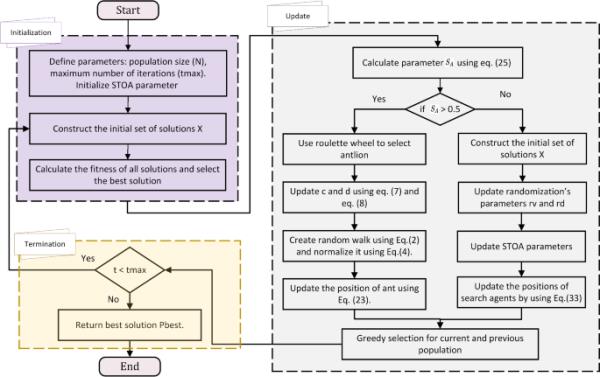
所提出的ST-AL方法流程图
在本节中,通过两个实验来评估所提出的ST-AL算法的质量:(1)将其作为一种全局优化方法来发现CEC2020基准函数的最优值,(2)将所提出的算法作为一种特征选择方法。各实验参数设置如表2所示。将ST-AL与PSO (Kennedy and Eberhart 1995)、GWO (Mirjalili et al. 2014)、HHO (Heidari et al. 2019)、MFO (Mirjalili 2015b)、MPA (Faramarzi et al. 2020)以及原始的ALO和STOA等流行算法进行了比较。每种算法的设置如表3所示。正如Arcuri和Fraser(2013)的作者所证明的,将算法参数设置为默认值是一种合理且可接受的做法。所有结果都是在一台CPU 2.67G、内存8.00G、运行64位操作系统的Intel Corei7计算机上使用Matlab 2021b计算的。
表2各实验参数设置
表3竞争算法参数设置
采用几种统计测量来评估所提出的ST-AL方法的性能。
1.
均值:表示优化算法的速度,因此已经应用了M次,定义如下:
(34)
式中,表示第i次操作生成的最优解。
2.
Best表示优化算法在M次独立操作中获得的最小(或最佳)适应度函数值。其计算如式(35)所示
(35)
3.
最差(Worst)计算为优化算法在M次独立操作中产生的最大(最差值)适应度函数值,如式(36)所示。
(36)
4.
标准偏差(Std)定义优化算法的鲁棒性和稳定性如下:(1)当Std值较小时,表示优化算法总是收敛于同一解,反之,当Std值较大时,表示优化算法接近于随机结果,如式(37)所示:
(37)
在特征选择实验的评价中,使用了额外的度量:
5.
平均分类准确率():数据被正确分类的比率反映在准确率度量中。本研究中每种方法共运行30次,因此度量确定如下:
(38)
其中N为实例数,为实例i的分类器输出标签,为实例i的参考类标签,当两个输入标签相同时为1,否则为0的函数。
6.
平均选择大小()表示被选择特征的平均大小,如Eq.(39)所示。
(39)
其中表示原始数据集中的全部特征号。
7.
平均CPU时间()计算每个算法的平均CPU时间(毫秒)
(40)
请注意,STD也是根据所有其他度量来计算的:准确性、时间和所选特征的数量。每个度量的最佳值以粗体突出显示。
使用IEEE进化计算大会(CEC2020) (Mohamed et al. 2020a)中列出的一组标准基准来评估所提出的ST-AL算法的性能。许多元启发式算法的性能已经使用这些函数进行了研究(Houssein et al. 2021;Mohamed et al. 2020b)。如表4所示,CEC 2020基准函数包括10个测试函数,分为四类:单模态、多模态、混合和组合函数。所有算法都独立运行了30次,以确保公平的基准比较,并与使用30个搜索代理运行超过3000次迭代的竞争算法集合相比,展示了所提议的ST-AL的鲁棒性。函数求值的最大次数是90,000次(迭代次数乘以搜索代理的总数)。这项研究采用了多种测量方法。这些指标包括适应度值的最小值、最大值、平均值、标准差(SD)和Wilcoxon秩和P值。
表4 CEC2020基准函数图带健康评分的处方(Fi*)
5.2.1 统计结果分析
使用10个CEC 2020基准函数,维度为solution(),表5显示了所有竞争算法获得的适应度得分的最佳、最差、平均值和标准差(STD)。每个评估标准的最佳结果用粗体标出。结果表明,ST-AL算法在平均适应度值方面优于其他元启发式算法。由于它在七个测试功能(F1, F2, F3, F5, F7, F9和F10)上表现更好,而MPA仅在三个功能(F4, F6和F8)上表现最好。结果在标准差方面也显示出类似的趋势,ST-AL在5个基准函数上优于其他算法,而MPA在4个基准函数(F3、F4、F6和F9)上优于其他算法。将ST-AL算法与使用最佳和最差适应度指标的其他算法进行比较,显示出具有竞争力的性能。当考虑到最佳和最差适应度指标时,与其他算法相比,ST-AL算法显示出具有竞争力的性能。这说明了ST-AL算法的搜索能力和稳定性。尽管其他算法在特定的测试用例中优于ST-AL,但就整体性能测量而言,ST-AL仍然是明显的赢家。实验结果表明,ST-AL在解决绝大多数优化问题方面优于其他7种元启发式方法。
此外,ST-AL和其他元启发式算法的性能在20维的CEC2020上进行了评估,如表6所示。该表显示ST-AL在6个函数(F2、F5、F6、F7、F9和F10)中优于竞争对手算法。另一方面,MPA在F3、F4、F8三个功能上表现较好。ALO仅在函数F1中提供更好的性能。
Wilcoxon和检验是一种非参数检验,可用于检验配对算法的结果。零假设表明比较方法的结果是不可区分的。根据这种不同的观点,比较方法可以按等级区分。得出五个显著性水平(P)的估计Wilcoxon排名。如果,假设被验证为零,如果,假设被接受。P Wilcoxon均值和适应度结果如表7和表8所示。本文提出的ST-AL算法与其他算法有明显的不同。因此,所提出的ST-AL算法得到了巨大的发展。
表5 ST-AL与其他组的统计结果基于ce2020基准函数的启发式算法
表6 ST-AL与其他组的统计结果基于ce2020基准函数的启发式算法
表7 ST-AL与其他me关于CEC2020()的ta-启发式算法PWilcoxon秩和检验
表8 ST-AL与其他me关于CEC2020()的ta-启发式算法PWilcoxon秩和检验
5.2.2 有限公司收敛行为分析
收敛性检验是确定优化算法稳定性的关键步骤。因此,本文对所提出的ST-AL及其竞争对手进行了比较分析。本文提出的ST-AL算法和其他竞争算法对CEC ' 2020函数的收敛曲线如图2所示。从图中可以清楚地看出,ST-AL算法对于所有函数都达到了一个稳定的点。在少量的函数评估中,所提出的ST-AL算法比其他比较算法更快地获得所有CECs基准函数的全局解的最低平均值。在需要快速计算的应用中,如在线优化问题,这种快速收敛的ST-AL算法可以很容易地被描述为一种潜在的优化方法。
图2
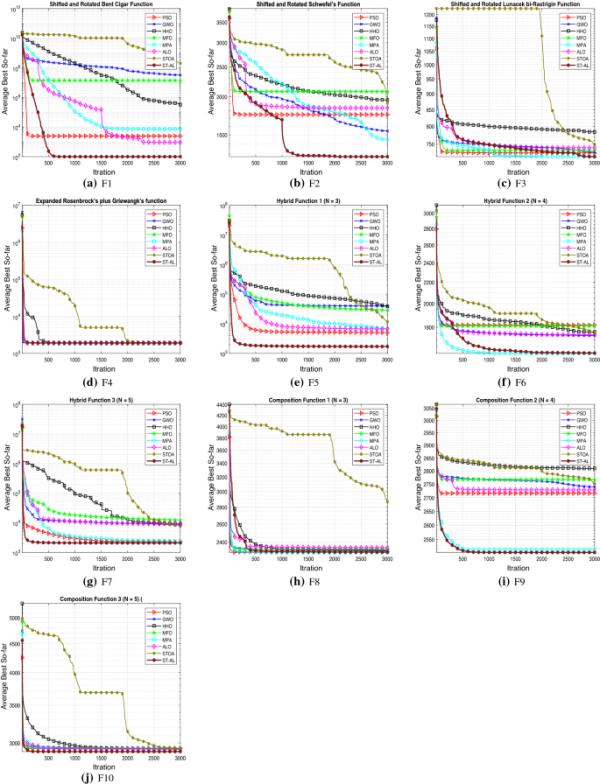
ST-AL与其他竞争对手的收敛曲线- cec2020
5.2.3 箱线图行为分析
箱线图分析可以显示数据分布的特征。这类函数有多个局部极小值;从而更好地理解结果的分布。箱形图是三个主要四分位数的数据分布的图形表示,即上、下和中四分位数。该算法的最小和最大数据点代表最小值和最大值,它们构成须的边缘。矩形的两端定义了上下四分位数。如果箱线图很窄,则数据点之间有很强的一致性。CEC ' 2010函数的箱线图如图3所示。与其他算法的分布相比,ST-AL算法在大多数函数中的箱线图都很窄,并且具有最低的值。因此,建议的ST-AL算法在考虑的绝大多数测试函数上优于其他竞争对手算法。
图3
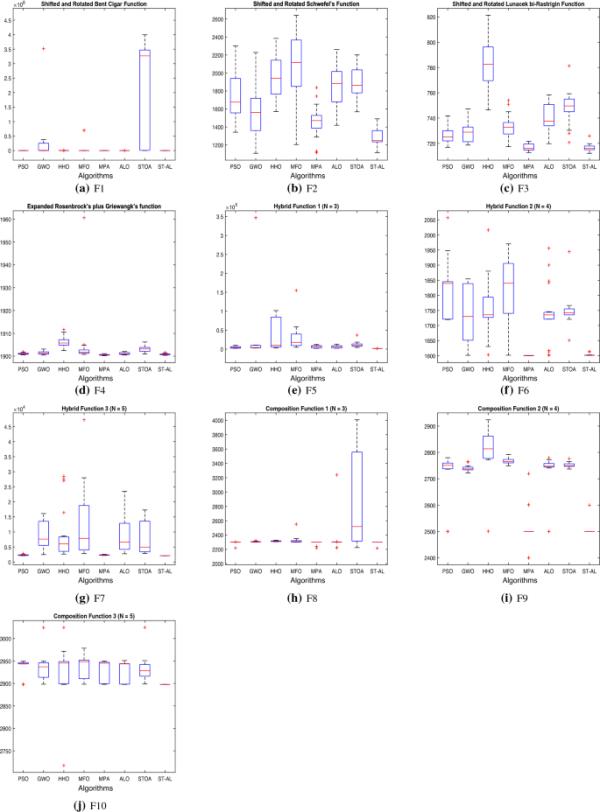
ST-AL与其他竞争对手的箱线图- cec2020
5.2.4 Exploration-exploitation分析
图4描述了在求解CEC 2020测试函数时寻找ST-AL维持的最优全局值时的勘探开发行为的二维视图,我们可以更好地解释勘探和开发的阶段。从图4可以明显看出,所提出的ST-AL在开始阶段具有较高的勘探开发比。尽管如此,花在寻找上的大部分时间都花在了过程的开发阶段。这种行为证明了所提出的ST-AL能够有效地平衡勘探和开发阶段。
图4
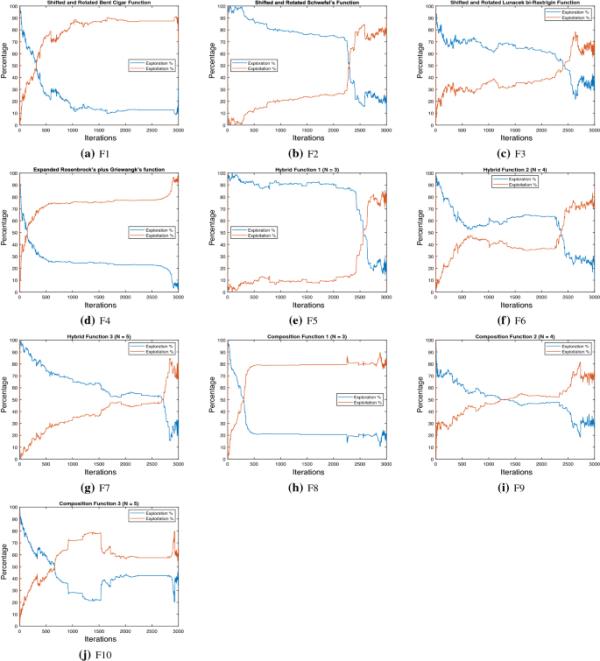
ST-AL法勘探开发曲线- cec2020
本节在特征选择上采用了所提出的混合ST-AL方法。这是一个NP-hard组合问题。假设数据集D有D个特征,则可能的特征子集的个数为(Eid 2018)。然后,使用ST-AL方法来发现最优可能的特征子集。根据所提出的方法,使用特征数和分类错误率来计算适应度值。适应度函数的数学公式为(Mafarja and Mirjalili 2017):
(41)
其中CR(D)表示错误率(使用KNN分类器计算),| D |表示原始特征集,|FS|表示选择的特征。和的取值范围为[0,1]。和分别为错误率和选择率的权重,其中为的补。如文献所述,控制参数和分别设置为0.99和0.001 (Kumar和Kaur 2020)。
在本实验中,通过与其他元启发式特征选择算法进行比较,对确定最佳特征子集的ST-AL方法进行了评估。这些算法在14个不同的数据集上进行了测试,每个数据集都有不同的类型。这些算法的参数设置与表3中定义的相同。从UCI机器学习存储库Asuncion(2007)中检索到本研究中使用的数据集。表9提供了研究中使用的每个数据集的简要概述。此外,本工作还使用了不同的评估标准来评估ST-AL方法的性能,例如:评估适应度函数值、根据所选特征评估分类器的准确性、所选特征的大小以及计算时间,如第5.1节所示。
表9 UCI基准数据集
5.3.1 UCI数据集的结果和讨论
比较方法适应度函数的均值和标准差如表10所示。实验结果表明,所提出的ST-AL算法取得了较好的效果。在75%的数据集上,ST-AL具有最佳的平均结果(16个数据集中的12个)。同样值得注意的是,在三个数据集(IonosphereEW、WineEW和Zoo数据集)中,MPA在平均适应度函数值方面优于其他算法。ST-AL是该数据集的次优算法。对于SonarEW数据集,GWO的性能优于竞争对手。ST-AL是该数据集的次优算法。所产生的结果证明了所提出的ST-AL解决各种特征选择问题的能力。另一方面,通过分析标准差,与其他策略相比,ST-AL方法对大多数数据集具有更强的鲁棒性。Std值证明了所提出的ST-AL在低分布的多次运行中产生的值接近,这表明所提出的ST-AL方法对于处理不同的特征选择问题是一种强大的方法。在Std测量中,ST-AL在14个数据集中的12个中获得最佳值。图5显示了所有算法的适应度值的平均值。
表10拟ST-AL与其他竞争对手的适应度值均值和标准差
图5
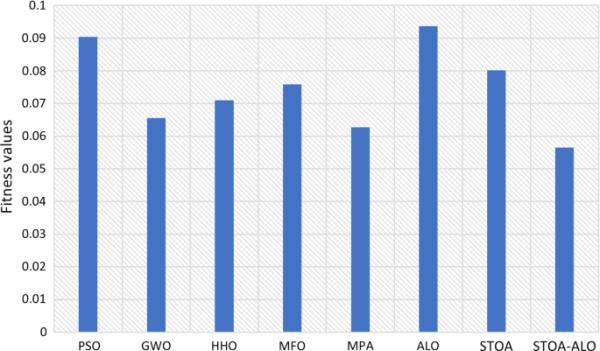
所有测试数据集的适应度值的平均值
表11显示了ST-AL和在相同设置下评估的其他算法之间的精度结果的比较。ST-AL在16个测试数据集中的6个上表现优于其他数据集,而MPA在16个数据集中的2个(PenglungEW, ionosphere eew)上表现最好。有7个数据集的MPA和ST-AL结果相同。ST-AL算法的性能也优于标准的STOA和ALO算法。图6显示了所有方法的准确度结果的平均值。与所有其他方法相比,ST-AL表现最好。实验结果表明,所提出的ST-AL方法选择了信息量最大、精度值较高的特征。
表11所提出的ST-AL和其他竞争对手的准确度均值和标准差
图6
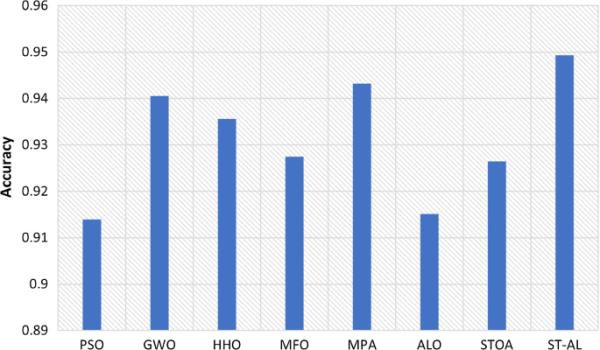
测量所有测试数据集的平均准确度
表12比较了ST-AL和竞争算法分类器对相同UCI数据集选择的平均特征数量。本研究使用了16个数据集,与其他优化器相比,ST-AL在7个数据集上获得的选择特征的平均数量是最好的。而STOA方法在6个数据集上获得了最好的结果。MPA和GWO分别为WineEW和exacly2两个数据集提供了最少一组选定的特性。与其他竞争方法相比,图7显示,传统STOA方法获得的特征数量最少,而ST-AL方法获得的第二选择特征数量最多。基于对标准偏差的检验,与其他方法相比,ST-AL对大多数数据集来说是一种可靠的方法。
表12所提出的ST-AL和其他竞争者的选择特征的均值和标准差
图7
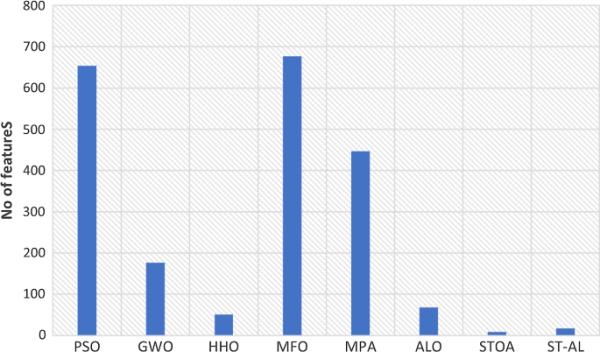
所有方法所选特征的平均值
比较方法的计算时间见表13。与其他方法相比,STOA方法具有最短的执行时间和最快的速度。如图8所示,就执行时间的速度而言,所提出的ST-AL方法几乎是第二种方法。由于其组合结构,该方法需要一定的时间来发现最优解,并且这类问题不需要实际的执行时间。
表13计算平均值和标准最终的时间
图8
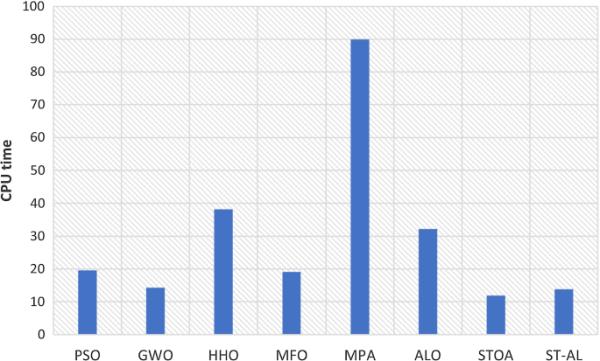
所有方法计算时间的平均值
图9和图10描绘了平均适应度值和竞争算法的收敛曲线和箱线图。可以观察到,将STOA和ALO集成在一起的ST-AL方法提高了向最优解收敛的速度。这可以注意到,例如:Exactly, Exactly2, Lymphography, SpectEW, CongressEW, Vote, HeartEW, M-of-n, base_Brain_T21和base_leuk1。此外,从箱线图可以看出,ST-AL的箱形最低。
图9
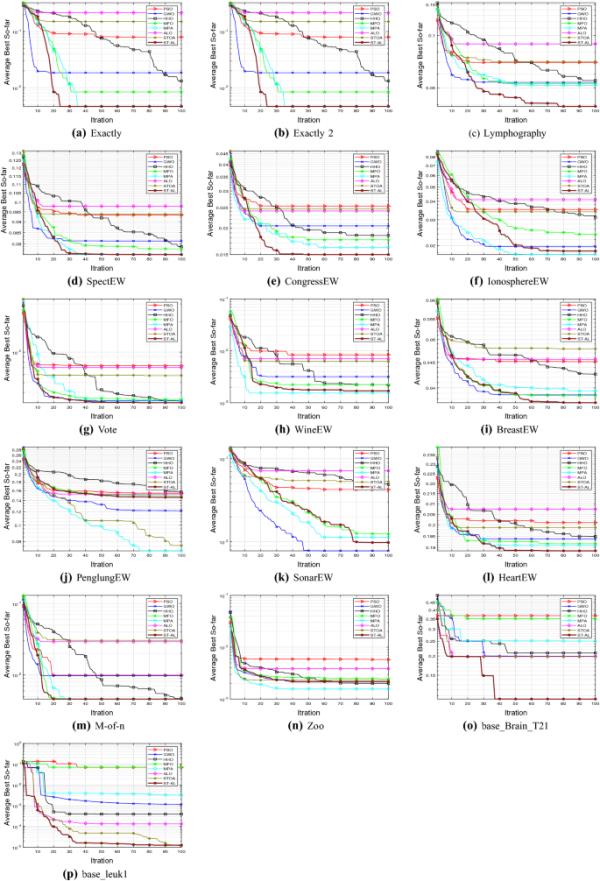
ST-AL与其他竞争对手的收敛曲线- uci数据集
图10
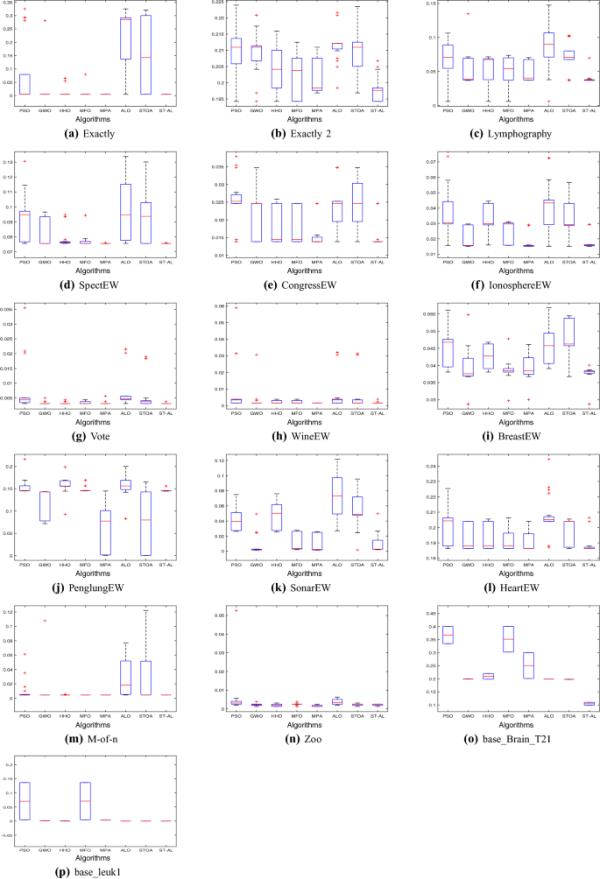
ST-AL与其他竞争对手的箱线图- uci数据集
根据评估指标和大多数测试用例,与其他竞争对手的方法相比,建议的ST-AL方法显示出显著的改进。STOA和ALO的结合是ST-AL方法令人印象深刻的结果的主要原因。总的来说,我们发现所提出的ST-AL方法给出了最好的结果,并被证明是一种高效的优化策略,可以处理不同的特征选择问题。
5.3.2 与最先进的特征选择方法的比较
本节将提出的ST-AL方法与最近与特征选择相关的文献中报道的其他混合方法进行比较。在表14中,ST-AL方法的精度值与近期文献中报道的各种混合特征选择算法进行了比较,包括ISOA (Ewees等人,2022)、WOASA (Mafarja和Mirjalili, 2017)、SCHHO (Hussain等人,2021)、GWOPSO (al - tashi等人,2019)、ASGW (Mafarja等人,2020)和GWOCrowSA (Arora等人,2019)。如表14所示,与文献中其他混合方法相比,ST-AL方法获得了最多的信息特征,从而获得了最高的分类精度,因为ST-AL方法在16个数据集中的12个数据集上更准确。同样,表15显示了与其他混合方法相比,使用ST-AL选择的特征数量。这一比较表明,所提出的ST-AL方法选择的特征数量明显低于文献中提出的其他混合方法,因为它在16个数据集中的6个数据集中获得的属性数量最少,精度值最高。
表14比较研究基于分类器的准确率,采用了最先进的特征选择方法
表15比较研究基于所选特征的大小,采用最先进的特征选择方法
提出了一种基于灰项优化算法(STOA)和蚁狮优化算法(ALO)的新型混合优化算法,用于处理函数优化问题和特征选择问题。在提出的ST-AL中,采用了四种策略来提高STOA的效率。第一种策略是使用控制随机化参数,它在平衡勘探开采阶段和避免陷入局部最优和过早收敛方面起着重要作用。第二种策略是基于ALO算法开发新的探索阶段,其中ALO算法被称为合理的探索策略。第三种策略是通过修改位置更新主方程来增强STOA开发阶段。最后一种策略是利用贪婪选择来忽略生成的不良种群,防止算法偏离已有的有希望的区域。为了评估ST-AL算法的有效性,在10个基准函数和16个数据集上进行了实验,作为特征选择方法。然后,将其与MPA、MFO、HHO、GWO、PSO、ALO和STOA等7种原始的元启发式算法进行比较。实验结果表明,ST-AL算法总体上优于其他7种比较算法,证明了其解决优化问题的能力和稳定性。在特征选择方面,所提出的ST-AL在75%的数据集上取得了平均最佳结果。因此,ST-AL可以作为一种有效的优化方法来解决各种特征选择问题。在未来的工作中,所提出的混合算法可用于解决现实场景中更现实的挑战。
下载原文档:https://link.springer.com/content/pdf/10.1007/s00500-022-07115-7.pdf
为您推荐:
- 罗阿诺克布兰登大道发生车祸,一人死亡,一人住院 2025-07-02
- 在第一阶段,监管机构提出了一个选择每日T+0结算周期(当日下午1:30前交易),当日下午4:30前完成资金及证券结算。 2025-07-02
- 美国联邦航空局将对波音公司进行审计,原因是飞机在飞行途中被撞飞 2025-07-01
- 普京前往靠近乌克兰边境的俄罗斯军事总部 2025-07-01
- 最后的订单吗?英国酒吧受到成本上涨和口味变化的冲击 2025-07-01
- 总部位于科克的招聘平台,旨在帮助陷入困境的公司找到专业人才 2025-07-01


